Yang–Mills existence and mass gap
In mathematics, the Yang-Mills existence and mass gap problem is an unsolved problem and one of the seven Millennium Prize Problems defined by the Clay Mathematics Institute which has offered a prize of US$1,000,000 to a person solving it.
The problem is phrased as follows:
- Yang–Mills Existence and Mass Gap. Prove that for any compact simple gauge group G, a non-trivial quantum Yang–Mills theory exists on
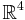and has a mass gap Δ > 0. Existence includes establishing axiomatic properties at least as strong as those cited in [45, 35].
In this statement, Yang–Mills theory is the (non-Abelian) quantum field theory underlying the Standard Model of particle physics; 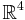is Euclidean 4-space; the mass gap Δ is the mass of the least massive particle predicted by the theory. Therefore, the winner must first prove that Yang–Mills theory exists and that it satisfies the standard of rigor that characterizes contemporary mathematical physics, in particular constructive quantum field theory, which is referenced in the papers 45 and 35 cited in the official problem description by Jaffe and Witten. The winner must then prove that the mass of the least massive particle of the force field predicted by the theory is strictly positive. For example, in the case of G=SU(3) - the strong nuclear interaction - the winner must prove that glueballs have a lower mass bound, and thus cannot be arbitrarily light.
Contents |
Background
| “ | [...] one does not yet have a mathematically complete example of a quantum gauge theory in four-dimensional space-time, nor even a precise definition of quantum gauge theory in four dimensions. Will this change in the 21st century? We hope so! | ” |
|
—From the Clay Institute's official problem description by Arthur Jaffe and Edward Witten. |
||
Most known and nontrivial (i.e. interacting) quantum field theories in 4 dimensions are effective field theories with a cutoff scale. Since the beta-function is positive for most models, it appears that most such models have a Landau pole as it is not at all clear whether or not they have nontrivial UV fixed points. This means that if such a QFT is well-defined at all scales, as it has to be to satisfy the axioms of axiomatic quantum field theory, it would have to be trivial (i.e. a free field theory).
Quantum Yang-Mills theory with a non-abelian gauge group and no quarks is an exception, because asymptotic freedom characterizes this theory, meaning that it has a trivial UV fixed point. Hence it is the simplest nontrivial constructive QFT in 4 dimensions. (QCD is a more complicated theory because it involves quarks.)
It has already been well proven—at least at the level of rigor of theoretical physics but not that of mathematical physics—that the quantum Yang–Mills theory for a non-abelian Lie group exhibits a property known as confinement. This property is covered in more detail in the relevant QCD articles (QCD, color confinement, lattice gauge theory, etc.), although not at the level of rigor of mathematical physics. A consequence of this property is that beyond a certain scale, known as the QCD scale (more properly, the confinement scale, as this theory is devoid of quarks), the color charges are connected by chromodynamic flux tubes leading to a linear potential between the charges. Hence free color charge and free gluons cannot exist. In the absence of confinement, we would expect to see massless gluons, but since they are confined, all we see are color-neutral bound states of gluons, called glueballs. If glueballs exist, they are massive, which is why we expect a mass gap.
Results from lattice gauge theory have convinced many that quantum Yang–Mills theory for a non-abelian Lie group model exhibits confinement—as indicated, for example, by an area law for the falloff of the vacuum expectation value (VEV) of a Wilson loop. However, these methods and results are not mathematically rigorous.
See also
References
- Arthur Jaffe and Edward Witten "Quantum Yang-Mills theory." Official problem description.